분류(Classification)에서의 성능 평가 지표에 대해 정리해보려한다.
분류(Classification) 성능 평가 지표
- 정확도(Accuracy)
- 오차행렬(Confusion Matrix)
- 정밀도(Precision)
- 재현율(Recall)
- F1 스코어
- ROC AUC
정확도(Accuracy)
정확도는 모델이 올바르게 예측한 샘플의 비율로 정의된다. 전체 예측한 샘플 중 올바르게 예측한 샘플의 수를 전체 샘플 수로 나눈 값으로 계산할 수 있다.
\[정확도(Accuracy)= \frac{예측\,결과가\,동일한\,데이터\,건수} {전체 \,예측\,데이터\,건수}\]정확도만으로 판단하면 안되는 이유
정확도는 비교적으로 쉽고, 직관적으로 모델 예측 성능을 나타내는 평가 지표이다. 하지만, 정확도는 불균형한 레이블 값 분포에서 ML 모델의 성능을 판단할 경우 모델의 성능을 왜곡할 수 있기 때문에 정확도 수치 하나만 가지고 성능을 평가하는 것은 적합하지 않다.
오차 행렬(Confusion Matrix)
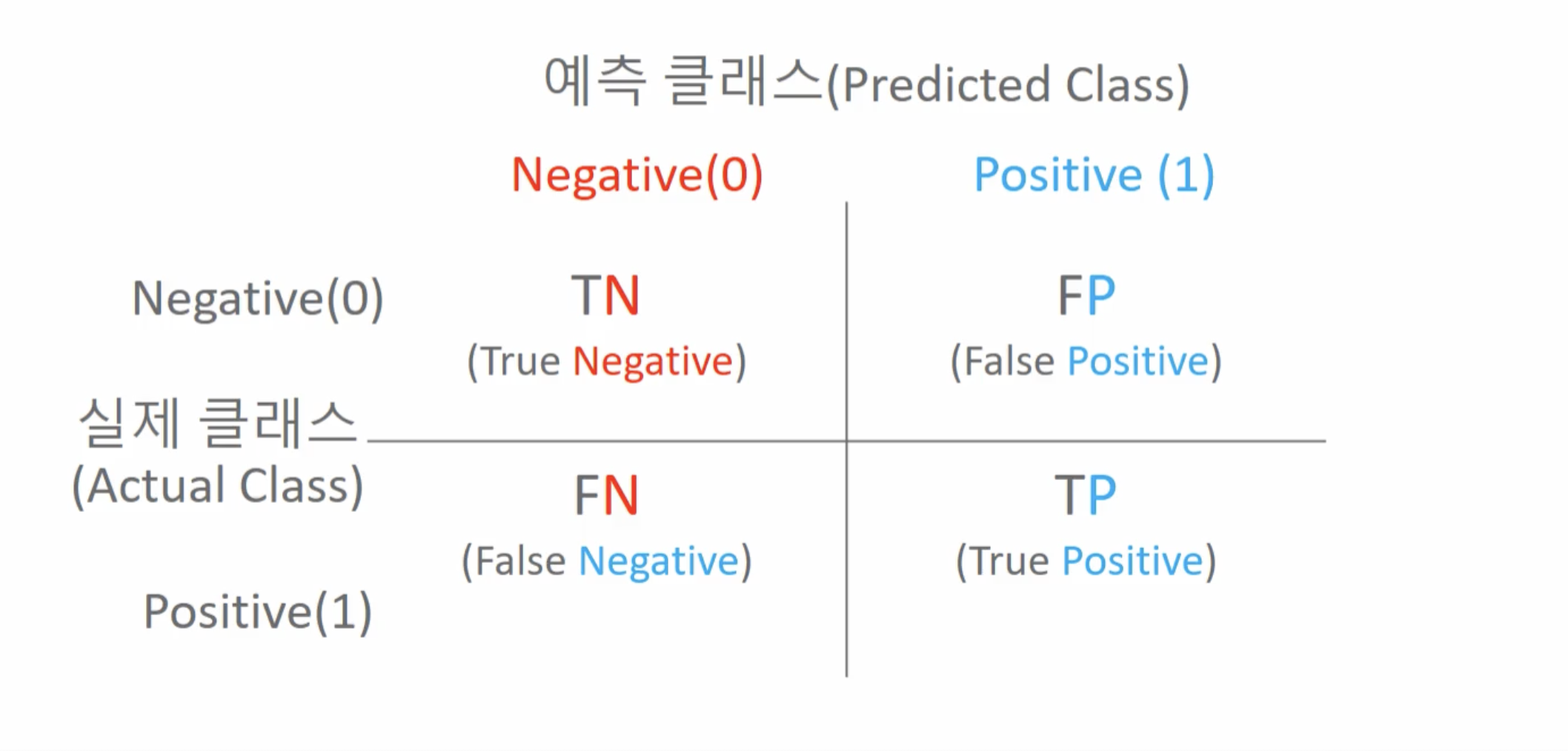
오차 행렬은 이진 분류의 예측 오류가 얼마인지와 더불어 어떠한 유형의 예측 오류가 발생하고 있는지를 함께 나타내는 지표이다.
- TN(True Negative) : 실제 값이 True, 예측 값이 Negative(실제 False인 답을 False로 예측 : 정답)
- FP(False Positive) : 실제 값이 False, 예측 값이 Postive(실제 False인 답을 True로 예측 : 오답)
- FN(False Negative) : 실제 값이 False, 예측 값이 Negative(실제 True인 답을 False로 예측 : 오답)
- TP(True Positive) : 실제 값이 True, 예측 값이 Positive(실제 True인 답을 True로 예측 : 정답)
정확도를 오차 행렬 지표를 이용한 식으로 나타내면 위의 식 처럼 나타낼 수 있다.
정밀도(Precision)
정밀도는 예측을 Positive로 한 대상 중에 예측과 실제 값이 Positvie로 일치한 데이터의 비율을 말한다.
\[정밀도(Precision) = \frac{TP}{FP\,+\,TP}\]위와 같은 식으로 표현이 가능하다. 정밀도는 쉽게 말해서 암 판별 모델이 암이 양성이라고 판별했는데, 실제 암이 양성일 비율이다.
정밀도가 상대적으로 더 중요한 지표의 경우
실제 Negative 데이터 예측을 Positive로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우
ex) 스팸 메일
재현율(Recall)
재현율은 실제 값이 Positive인 대상중에 예측과 실제 값이 Positvie로 일치한 데이터의 비율을 말한다.
\[재현율(Recall) = \frac{TP}{FN\,+\,TP}\]위와 같은 식으로 표현이 가능하다. 정밀도와 같은 예를 들어서, 재현율은 실제 암이 양성이고, 암 판별 모델이 암이 양성이라고 판별할 비율이다.
재현율이 상대적으로 더 중요한 지표의 경우
실제 Positive 데이터 예측을 Negative로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우 ex) 암 진단, 금융사기 판별
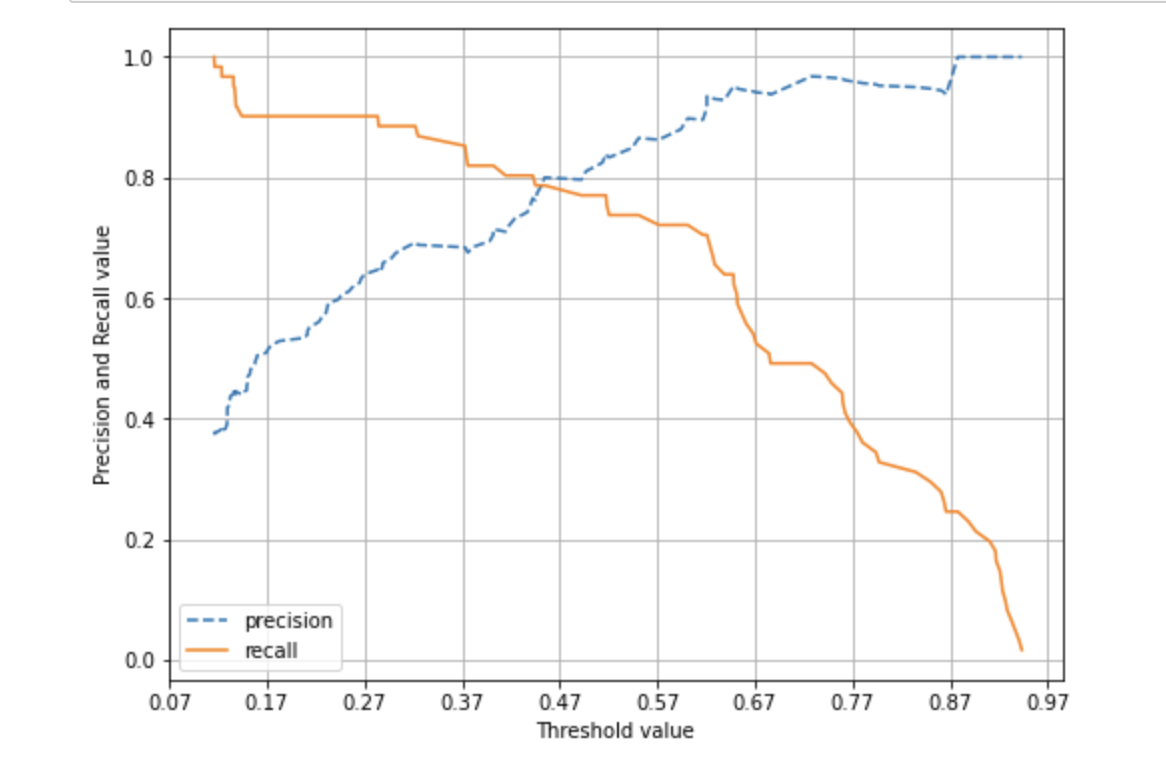
정밀도와 재현율의 Trade-off
분류의 결정 임계값(Threshold)을 조정해 정밀도 또는 재현율의 수치를 높일 수 있다. 하지만, 위의 그래프를 보면 알 수 있듯이 정밀도와 재현율은 상호 보완적인 평가 지표이기 때문에 어느 한 쪽을 강제로 높이면 다른 하나의 수치는 떨어지기 쉽다. 이를 정밀도와 재현율의 Trade-off라고 한다.
F1 스코어
F1 스코어는 정밀도와 재현율을 결합한 지표이다. F1 스코어가 상대적으로 높다는 것은 정밀도와 재현율이 어느 한쪽으로 치우치지 않는다는 것을 의미한다.
\[F1 = \frac{2}{\frac{1}{recall}\,+\,\frac{1}{precision}} = 2\,\times\,\frac{precision\,*\,recall}{precision\,+\,recall}\]F1 스코어는 위의 식으로 나타낼 수 있다.
ROC와 AUC
ROC 곡선(Receiver Operation Characteristic Curve)과 이에 기반한 AUC 스코어는 이진 분류의 예측 성능 측정에서 중요하게 사용되는 지표이다. 일반적으로 의학 분야에서 많이 사용되지만, 머신러닝의 이진 분류 모델의 예측 성능을 판단하는 중요한 평가 지표이기도 하다.
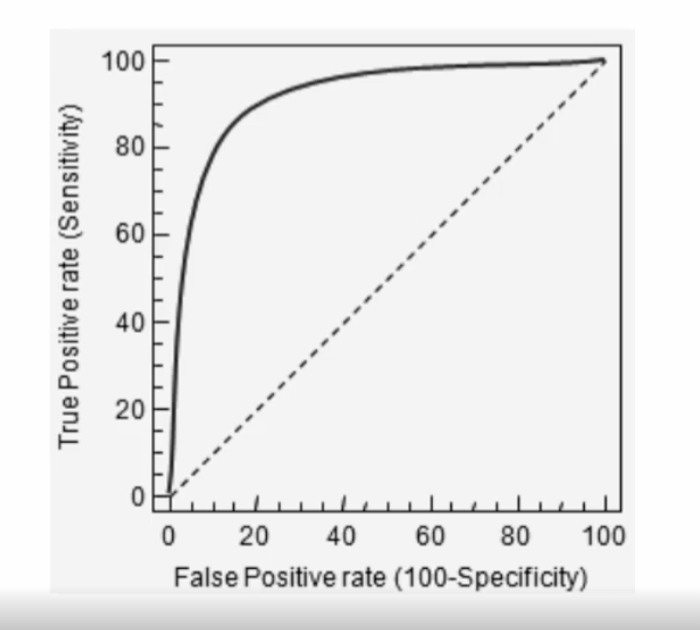
ROC 곡선은 FPR(False Positive Rate)이 변할 때 TPR(True Positive Rate)이 어떻게 변하는지를 나타내는 곡선이다. FPR을 X축으로, TPR을 Y축으로 잡은 그래프이다.
AUC 값은 ROC 곡선 아래 영역의 면적을 구한 것으로 일반적으로 1에 가까울수록 좋은 수치이다.
X축을 나타내는 FPR은 실제 Negative를 잘못 예측한 비율이다. 즉, 실제는 Negative인데 Positive로 잘못 예측한 비율이다.
\[FPR = \frac{FP}{FP\,+\,TN}\]위의 식으로 FPR을 나타낼 수 있다.
Y축을 나타내는 TPR은 재현율을 나타내고 민감도라고도 불린다.
\[TPR = Recall = \frac{TP}{FN\,+\,TP}\]위의 식으로 TPR을 나타낼 수 있다.
느낀점
분류 성능 평가 지표는 머신러닝의 모델을 평가할 때 매우 중요하게 사용되는 지표이다. 처음에는 정확도만 높으면 좋은 모델인 줄 알고 정확도에만 의존했었는데, 정확도 하나로 모델 성능을 평가한다면 큰 문제가 발생한다는 것을 알게 되었다. 아직 정밀도, 재현율 ,F1 score, ROC AUC에 대한 개념이 잘 잡혀있지 않지만 매우 중요한 지표이므로 더 열심히 공부해야겠다.
참고한 사이트 및 강의
강의 : 파이썬 머신러닝 완벽 가이드